This article gives a brief introduction of the structure of a hash table, demonstrates hash flooding attack -- a common attack on it, and how to militate it when implementing this data structure.

Everybody loves hashmaps.

They provide a blazing fast average $O(1)$ access^* to associate any value to any key, asking for only two things in return: an equality comparer and a hash function, nothing more. This unique property makes hashmaps often more efficient than other associative data structures like search trees. As a result, hashmaps are nowadays one of the most used data structures in programming languages.

From the humble dict in Python, to databases and distributed systems, and even JavaScript objects, they're everywhere. They power database indexing systems, enable efficient caching mechanisms, and form the backbone of web frameworks for routing requests. Modern compilers use them for symbol tables, operating systems rely on them for process management, and virtually every web application uses them to manage user state.

Whether you're building a web server, parsing JSON values, dealing with configurations, or just counting word frequencies, chances are you'll reach for a hashmap. They've become so fundamental that many developers take their $O(1)$ magic for granted -- but the $1$ in $O(1)$ has got some strings^* attached.

The anatomy of a hashmap​

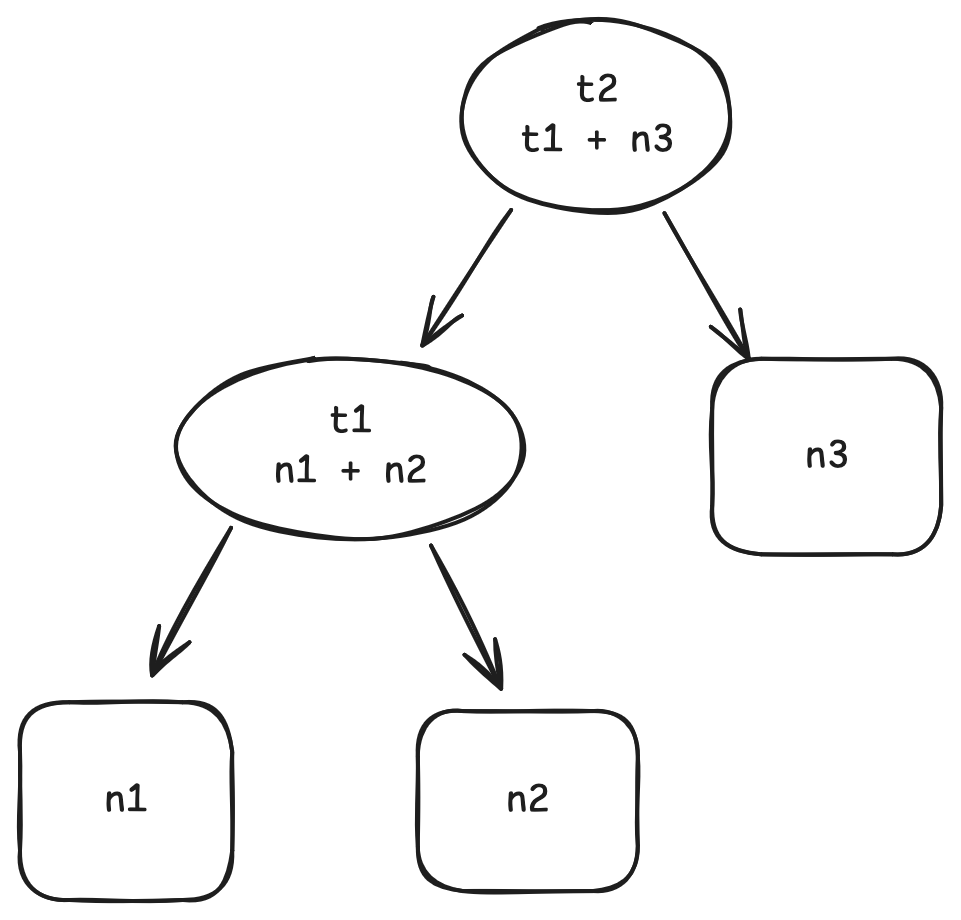
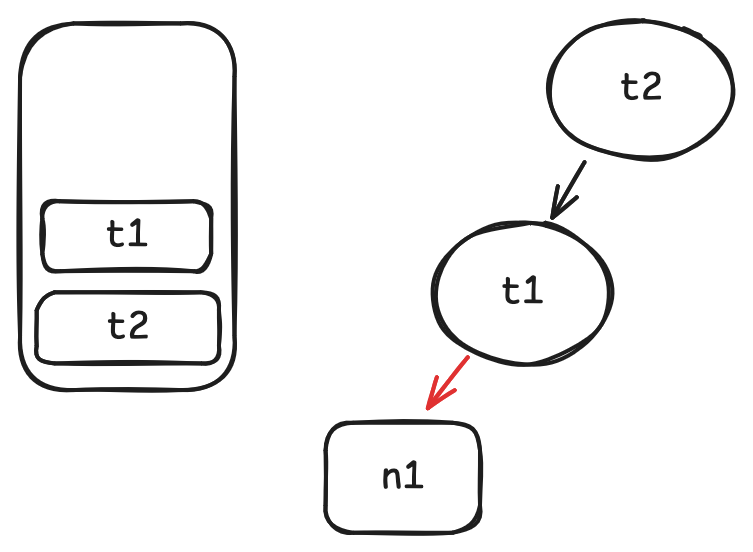
A hashmap is made of two parts: a bucket array and a hash function.

struct MyHashMap[K, V] {
  
Array[ChainingBucket[K, V]]
buckets : 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[
struct ChainingBucket[K, V] {
  values: Array[(K, V)]
}
Bucket[
type parameter K
K, 
type parameter V
V]]
  
(K) -> UInt
hash_fn : (
type parameter K
K) -> 
UInt
UInt
}

The bucket array contains a list of what we call "buckets". Each bucket stores some data we have inserted.

The hash function H associates each key with an integer. This integer is used to find an index in the bucket array to store our value. Usually, the index is derived by simply moduloing the integer with the size of the bucket array, i.e. index = H(key) % bucket_array_size. The hashmap expects the function to satisfy two important properties:

1. The same key is always converted to the same number. i.e., if a == b, then H(a) == H(b).

   This property ensures that, once we have found a bucket to insert using a key, we can always find the same bucket where it has been inserted, using the same key.

2. The resulting number is distributed uniformly across the space of possible results for different keys.

   This property ensures that different keys are unlikely to have the same associated integer, and in consequence, unlikely to be mapped to the same bucket in the array, allowing us to retrieve the value efficiently.

Now, you may ask, what would happen if two keys map to the same bucket? This comes to the realm of hash collisions.

Hash collisions​

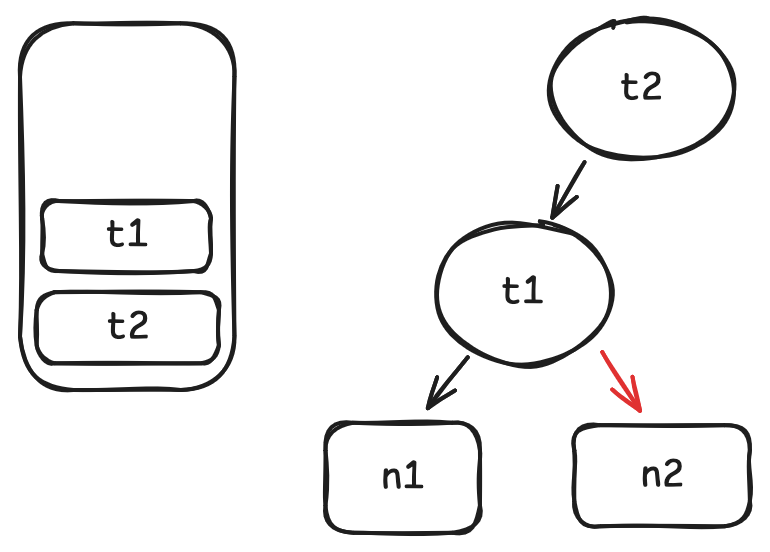
When two keys have the same hash value, or more broadly, when two keys map to the same bucket, a hash collision occurs.

As hashmaps determines everything based on the hash value (or bucket index), the two keys now look the same to the hashmap itself -- they should be put into the same place, but still unequal enough to not overwriting each other.

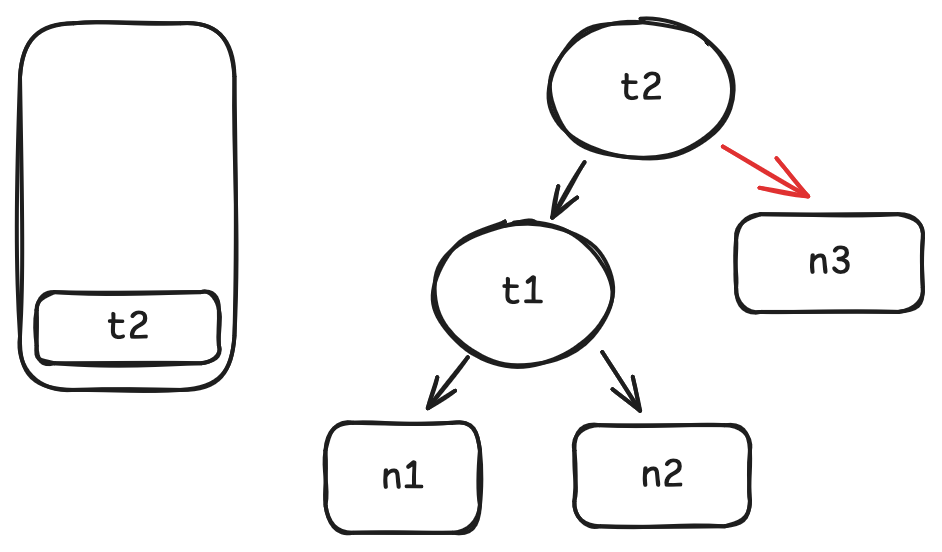
Hashmap designers have a couple of strategies to deal with collisions, which fall into one of the two broad categories:

• The chaining method puts these keys in the same bucket. Each bucket now may contain the data for a number of keys, instead of just one. When searching for a colliding key, all keys in the bucket are searched at once.

  struct ChainingBucket[K, V] {
    
  Array[(K, V)]
  values : 
  type Array[T]
  An Array is a collection of values that supports random access and can
  grow in size.
  Array[(
  type parameter K
  K, 
  type parameter V
  V)]
  }
  

  Java's HashMap is a popular example of this approach.

• The open addressing method still has one key per bucket, but uses a separate strategy to choose another bucket index when keys collide. When searching for a key, buckets are searched in the order of the strategy until the it is obvious that there are no more keys that could match.

  struct OpenAddressBucket[K, V] {
    
  Int
  hash: 
  Int
  Int
    
  K
  key: 
  type parameter K
  K
    
  V
  value: 
  type parameter V
  V
  }
  

  MoonBit's standard library Map is an example of this approach.

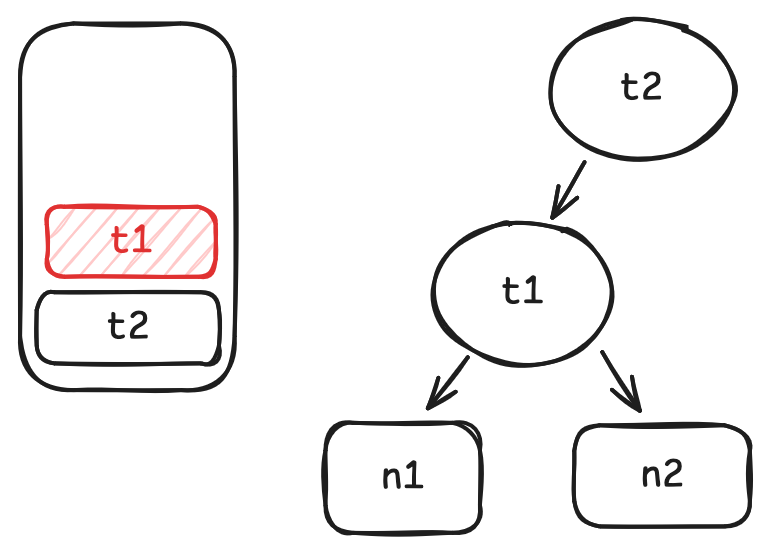
Either case, when a hash collision happens, we have no choice but to search through everything corresponding to the bucket we've found, to determine whether the key we are looking for is there or not.

Using a chaining hashmap (for simplicity), the whole operation looks something like this:

typealias 
struct ChainingBucket[K, V] {
  values: Array[(K, V)]
}
ChainingBucket as Bucket

/// Search for the place where the key is stored.
///
/// Returns `(bucket, index, number_of_searches_done)`
fn[K : 
trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq, V] 
struct MyHashMap[K, V] {
  buckets: Array[ChainingBucket[K, V]]
  hash_fn: (K) -> UInt
}
MyHashMap::
(self : MyHashMap[K, V], key : K) -> (Int, Int?, Int)
Search for the place where the key is stored.
Returns (bucket, index, number_of_searches_done)
search(
MyHashMap[K, V]
self : 
struct MyHashMap[K, V] {
  buckets: Array[ChainingBucket[K, V]]
  hash_fn: (K) -> UInt
}
MyHashMap[
type parameter K
K, 
type parameter V
V], 
K
key : 
type parameter K
K) -> (
Int
Int, 
Int
Int?, 
Int
Int) {
  let 
UInt
hash = (
MyHashMap[K, V]
self.
(K) -> UInt
hash_fn)(
K
key)
  let 
Int
bucket = (
UInt
hash 
(self : UInt, other : UInt) -> UInt
Calculates the remainder of dividing one unsigned integer by another.
Parameters:

self : The unsigned integer dividend.
other : The unsigned integer divisor.
Returns the remainder of the division operation.
Throws a panic if other is zero.
Example:
  let a = 17U
  let b = 5U
  inspect(a % b, content="2") // 17 divided by 5 gives quotient 3 and remainder 2
  inspect(7U % 4U, content="3")
% 
MyHashMap[K, V]
self.
Array[ChainingBucket[K, V]]
buckets.
(self : Array[ChainingBucket[K, V]]) -> Int
Returns the number of elements in the array.
Parameters:

array : The array whose length is to be determined.
Returns the number of elements in the array as an integer.
Example:
  let arr = [1, 2, 3]
  inspect(arr.length(), content="3")
  let empty : Array[Int] = []
  inspect(empty.length(), content="0")
length().
(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint()).
(self : UInt) -> Int
reinterpret the unsigned int as signed int
For number within the range of 0..=2^31-1,
the value is the same. For number within the range of 2^31..=2^32-1,
the value is negative
reinterpret_as_int()
  // Result
  let mut 
Int?
found_index = 
Int?
None
  let mut 
Int
n_searches = 0
  // Search through all key-value pairs in the bucket.
  for 
Int
index, 
(K, V)
keyvalue in 
MyHashMap[K, V]
self.
Array[ChainingBucket[K, V]]
buckets
(Array[ChainingBucket[K, V]], Int) -> ChainingBucket[K, V]
Retrieves an element from the array at the specified index.
Parameters:

array : The array to get the element from.
index : The position in the array from which to retrieve the element.
Returns the element at the specified index.
Throws a panic if the index is negative or greater than or equal to the
length of the array.
Example:
  let arr = [1, 2, 3]
  inspect(arr[1], content="2")
[bucket].
Array[(K, V)]
values {
    
Int
n_searches 
(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
  inspect(42 + 1, content="43")
  inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+= 1
    if 
(K, V)
keyvalue.
K
0 
(_ : K, _ : K) -> Bool
== 
K
key { // Check if the key matches.
      
Int?
found_index = 
(Int) -> Int?
Some(
Int
index)
      break
    }
  }
  return (
Int
bucket, 
Int?
found_index, 
Int
n_searches)
}

/// Insert a new key-value pair.
///
/// Returns the number of searches done.
fn[K : 
trait Eq {
  equal(Self, Self) -> Bool
  op_equal(Self, Self) -> Bool
}
Trait for types whose elements can test for equality
Eq, V] 
struct MyHashMap[K, V] {
  buckets: Array[ChainingBucket[K, V]]
  hash_fn: (K) -> UInt
}
MyHashMap::
(self : MyHashMap[K, V], key : K, value : V) -> Int
Insert a new key-value pair.
Returns the number of searches done.
insert(
MyHashMap[K, V]
self : 
struct MyHashMap[K, V] {
  buckets: Array[ChainingBucket[K, V]]
  hash_fn: (K) -> UInt
}
MyHashMap[
type parameter K
K, 
type parameter V
V], 
K
key : 
type parameter K
K, 
V
value : 
type parameter V
V) -> 
Int
Int {
  let (
Int
bucket, 
Int?
index, 
Int
n_searches) = 
MyHashMap[K, V]
self.
(self : MyHashMap[K, V], key : K) -> (Int, Int?, Int)
Search for the place where the key is stored.
Returns (bucket, index, number_of_searches_done)
search(
K
key)
  if 
Int?
index is 
(Int) -> Int?
Some(
Int
index) {
    
MyHashMap[K, V]
self.
Array[ChainingBucket[K, V]]
buckets
(Array[ChainingBucket[K, V]], Int) -> ChainingBucket[K, V]
Retrieves an element from the array at the specified index.
Parameters:

array : The array to get the element from.
index : The position in the array from which to retrieve the element.
Returns the element at the specified index.
Throws a panic if the index is negative or greater than or equal to the
length of the array.
Example:
  let arr = [1, 2, 3]
  inspect(arr[1], content="2")
[bucket].
Array[(K, V)]
values
(Array[(K, V)], Int, (K, V)) -> Unit
Sets the element at the specified index in the array to a new value. The
original value at that index is overwritten.
Parameters:

array : The array to modify.
index : The position in the array where the value will be set.
value : The new value to assign at the specified index.
Throws an error if index is negative or greater than or equal to the length
of the array.
Example:
  let arr = [1, 2, 3]
  arr[1] = 42
  inspect(arr, content="[1, 42, 3]")
[index] = (
K
key, 
V
value)
  } else {
    
MyHashMap[K, V]
self.
Array[ChainingBucket[K, V]]
buckets
(Array[ChainingBucket[K, V]], Int) -> ChainingBucket[K, V]
Retrieves an element from the array at the specified index.
Parameters:

array : The array to get the element from.
index : The position in the array from which to retrieve the element.
Returns the element at the specified index.
Throws a panic if the index is negative or greater than or equal to the
length of the array.
Example:
  let arr = [1, 2, 3]
  inspect(arr[1], content="2")
[bucket].
Array[(K, V)]
values.
(self : Array[(K, V)], value : (K, V)) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push((
K
key, 
V
value))
  }
  
Int
n_searches
}

This is the string attached to the $O(1)$ access magic -- we'd have to search through everything if we're unlucky. This gives the hashmap a worst-case complexity of $O(n)$, where $n$ is the number of keys in the hashmap.

Crafting a collision​

For most hash functions we use for hashmaps, unlucky collisions are rare. This means that we usually won't need to bother with the worst case scenario and enjoy the $O(1)$ speed for the vast majority of the time.

That is, unless someone, maybe some black-suited hackerman with some malicious intent, forces you into one.

Hash functions are usually designed to be deterministic and fast, so even without advanced cryptanalysis of the function itself, we can still find some keys that will collide with each other by brute force. ¹

fn 
(bucket_count : Int, target_bucket : Int, n_collision_want : Int, hash_fn : (String) -> UInt) -> Array[String]
find_collision(
  
Int
bucket_count : 
Int
Int,
  
Int
target_bucket : 
Int
Int,
  
Int
n_collision_want : 
Int
Int,
  
(String) -> UInt
hash_fn : (
String
String) -> 
UInt
UInt,
) -> 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[
String
String] {
  let 
Array[String]
result = []
  let 
UInt
bucket_count = 
Int
bucket_count.
(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint()
  let 
UInt
target_bucket = 
Int
target_bucket.
(self : Int) -> UInt
reinterpret the signed int as unsigned int, when the value is
non-negative, i.e, 0..=2^31-1, the value is the same. When the
value is negative, it turns into a large number,
for example, -1 turns into 2^32-1
reinterpret_as_uint()
  for 
Int
i = 0; ; 
Int
i = 
Int
i 
(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
  inspect(42 + 1, content="43")
  inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+ 1 {
    // Generate some string key.
    let 
String
s = 
Int
i.
(self : Int, radix~ : Int) -> String
Converts an integer to its string representation in the specified radix (base).
Example:
inspect((255).to_string(radix=16), content="ff")
inspect((-255).to_string(radix=16), content="-ff")
to_string(
Int
radix=36)
    // Calculate the hash value
    let 
UInt
hash = 
(String) -> UInt
hash_fn(
String
s)
    let 
UInt
bucket_index = 
UInt
hash 
(self : UInt, other : UInt) -> UInt
Calculates the remainder of dividing one unsigned integer by another.
Parameters:

self : The unsigned integer dividend.
other : The unsigned integer divisor.
Returns the remainder of the division operation.
Throws a panic if other is zero.
Example:
  let a = 17U
  let b = 5U
  inspect(a % b, content="2") // 17 divided by 5 gives quotient 3 and remainder 2
  inspect(7U % 4U, content="3")
% 
UInt
bucket_count
    let 
UInt
bucket_index = if 
UInt
bucket_index 
(self_ : UInt, other : UInt) -> Bool
< 0 {
      
UInt
bucket_index 
(self : UInt, other : UInt) -> UInt
Performs addition between two unsigned 32-bit integers. If the result
overflows, it wraps around according to the rules of modular arithmetic
(2^32).
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand to be added.
Returns the sum of the two unsigned integers, wrapped around if necessary.
Example:
  let a = 42U
  let b = 100U
  inspect(a + b, content="142")

  // Demonstrate overflow behavior
  let max = 4294967295U // UInt::max_value
  inspect(max + 1U, content="0")
+ 
UInt
bucket_count
    } else {
      
UInt
bucket_index
    }
    // Check if it collides with our target bucket.
    if 
UInt
bucket_index 
(self : UInt, other : UInt) -> Bool
Compares two unsigned 32-bit integers for equality.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand to compare with.
Returns true if both integers have the same value, false otherwise.
Example:
  let a = 42U
  let b = 42U
  let c = 24U
  inspect(a == b, content="true")
  inspect(a == c, content="false")
== 
UInt
target_bucket {
      
Array[String]
result.
(self : Array[String], value : String) -> Unit
Adds an element to the end of the array.
If the array is at capacity, it will be reallocated.
Example
  let v = []
  v.push(3)
push(
String
s)
      if 
Array[String]
result.
(self : Array[String]) -> Int
Returns the number of elements in the array.
Parameters:

array : The array whose length is to be determined.
Returns the number of elements in the array as an integer.
Example:
  let arr = [1, 2, 3]
  inspect(arr.length(), content="3")
  let empty : Array[Int] = []
  inspect(empty.length(), content="0")
length() 
(self_ : Int, other : Int) -> Bool
>= 
Int
n_collision_want {
        break
      }
    }
  }
  
Array[String]
result
}

Hash flooding attack​

With colliding values in hand, we (in the role of malicious hackermen) can now attack hashtables to constantly exploit their worst-case complexity.

Consider the following case: you are inserting keys into the same hashmap, but every key hashes into the same bucket. With each insert, the hashmap must search through all the existing keys in the bucket to determine whether the new key is already there.

The first insertion compares with 0 keys, the second with 1 key, the third compares with 2 keys, and the number of keys compared grows linearly with each insertion. For $n$ insertions, the total number of keys compared is:

$$0 + 1 + \dots + (n - 1) = \frac{n(n - 1)}{2} = \frac{n^2 + n}{2}$$

The total list of $n$ insertions now takes $O(n^2)$ compares to complete², as opposed to the average case of $O(n)$ compares. The operation will now take far more time than it ought to.

The attack is not just limited to insertion. Every time when an attacked key is being searched for, the same number of keys will be compared, so every single operation that would have been $O(1)$ now becomes $O(n)$. These hashmap operations that would otherwise take negligible time will now be severely slower, making the attacker far easier to deplete the program's resources than before.

This, is what we call a hash flooding attack, taken its name from it flooding the same bucket of the hashmap with colliding keys.

We can demonstrate this with the hashmap implementation we wrote earlier:

/// A simple string hasher via the Fowler-Noll-Vo hash function.
/// https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function
fn 
(s : String) -> UInt
A simple string hasher via the Fowler-Noll-Vo hash function.
https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function
string_fnv_hash(
String
s : 
String
String) -> 
UInt
UInt {
  // In reality this should directly operate on the underlying array of the string
  let 
Bytes
s_bytes = 
(str : StringView, bom? : Bool, endianness? : @encoding/utf16.Endian) -> Bytes
Encodes a string into a UTF-16 byte array.
Assuming the string is valid.
@encoding/utf16.encode(
String
s)
  let mut 
UInt
acc : 
UInt
UInt = 0x811c9dc5
  for 
Byte
b in 
Bytes
s_bytes {
    
UInt
acc = (
UInt
acc 
(self : UInt, other : UInt) -> UInt
Performs a bitwise XOR (exclusive OR) operation between two unsigned 32-bit
integers. Each bit in the result is set to 1 if the corresponding bits in the
operands are different, and 0 if they are the same.
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand.
Returns the result of the bitwise XOR operation.
Example:
  let a = 0xFF00U // Binary: 1111_1111_0000_0000
  let b = 0x0F0FU // Binary: 0000_1111_0000_1111
  inspect(a ^ b, content="61455") // Binary: 1111_0000_0000_1111
^ 
Byte
b.
(self : Byte) -> UInt
Converts a Byte to a UInt.
Parameters:

byte : The Byte value to be converted.
Returns the UInt representation of the Byte.
to_uint()) 
(self : UInt, other : UInt) -> UInt
Performs multiplication between two unsigned 32-bit integers. The result
wraps around if it exceeds the maximum value of UInt.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand.
Returns the product of the two unsigned integers. If the result exceeds the
maximum value of UInt (4294967295), it wraps around to the corresponding
value modulo 2^32.
Example:
  let a = 3U
  let b = 4U
  inspect(a * b, content="12")
  let max = 4294967295U
  inspect(max * 2U, content="4294967294") // Wraps around to max * 2 % 2^32
* 0x01000193
  }
  
UInt
acc
}

fn 
(n_buckets : Int, keys : Array[String], hash_fn : (String) -> UInt) -> Int
test_attack(
  
Int
n_buckets : 
Int
Int,
  
Array[String]
keys : 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array[
String
String],
  
(String) -> UInt
hash_fn : (
String
String) -> 
UInt
UInt,
) -> 
Int
Int {
  let 
MyHashMap[String, Int]
map = { 
Array[ChainingBucket[String, Int]]
buckets: 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array::
(Int, (Int) -> ChainingBucket[String, Int]) -> Array[ChainingBucket[String, Int]]
Creates a new array of the specified length, where each element is
initialized using an index-based initialization function.
Parameters:

length : The length of the new array. If length is less than or equal
to 0, returns an empty array.
initializer : A function that takes an index (starting from 0) and
returns a value of type T. This function is called for each index to
initialize the corresponding element.
Returns a new array of type Array[T] with the specified length, where each
element is initialized using the provided function.
Example:
  let arr = Array::makei(3, i => i * 2)
  inspect(arr, content="[0, 2, 4]")
makei(
Int
n_buckets, _ => { 
Array[(String, Int)]
values: [] }), 
(String) -> UInt
hash_fn }
  let mut 
Int
total_searches = 0
  for 
String
key in 
Array[String]
keys {
    
Int
total_searches 
(self : Int, other : Int) -> Int
Adds two 32-bit signed integers. Performs two's complement arithmetic, which
means the operation will wrap around if the result exceeds the range of a
32-bit integer.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns a new integer that is the sum of the two operands. If the
mathematical sum exceeds the range of a 32-bit integer (-2,147,483,648 to
2,147,483,647), the result wraps around according to two's complement rules.
Example:
  inspect(42 + 1, content="43")
  inspect(2147483647 + 1, content="-2147483648") // Overflow wraps around to minimum value
+= 
MyHashMap[String, Int]
map.
(self : MyHashMap[String, Int], key : String, value : Int) -> Int
Insert a new key-value pair.
Returns the number of searches done.
insert(
String
key, 0)
  }
  
Int
total_searches
}

test {
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("Demonstrate hash flooding attack")
  let 
Int
bucket_count = 2048
  let 
Int
target_bucket_id = 42
  let 
Int
n_collision_want = 1000

  //
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("First, try to insert non-colliding keys.")
  let 
Array[String]
non_colliding_keys = 
type Array[T]
An Array is a collection of values that supports random access and can
grow in size.
Array::
(Int, (Int) -> String) -> Array[String]
Creates a new array of the specified length, where each element is
initialized using an index-based initialization function.
Parameters:

length : The length of the new array. If length is less than or equal
to 0, returns an empty array.
initializer : A function that takes an index (starting from 0) and
returns a value of type T. This function is called for each index to
initialize the corresponding element.
Returns a new array of type Array[T] with the specified length, where each
element is initialized using the provided function.
Example:
  let arr = Array::makei(3, i => i * 2)
  inspect(arr, content="[0, 2, 4]")
makei(
Int
n_collision_want,
    
Int
i => (
Int
i 
(self : Int, other : Int) -> Int
Multiplies two 32-bit integers. This is the implementation of the *
operator for Int.
Parameters:

self : The first integer operand.
other : The second integer operand.
Returns the product of the two integers. If the result overflows the range of
Int, it wraps around according to two's complement arithmetic.
Example:
  inspect(42 * 2, content="84")
  inspect(-10 * 3, content="-30")
  let max = 2147483647 // Int.max_value
  inspect(max * 2, content="-2") // Overflow wraps around
* 37).
(self : Int, radix~ : Int) -> String
Converts an integer to its string representation in the specified radix (base).
Example:
inspect((255).to_string(radix=16), content="ff")
inspect((-255).to_string(radix=16), content="-ff")
to_string(
Int
radix=36))
  let 
Int
n_compares_nc = 
(n_buckets : Int, keys : Array[String], hash_fn : (String) -> UInt) -> Int
test_attack(
    
Int
bucket_count, 
Array[String]
non_colliding_keys, 
(s : String) -> UInt
A simple string hasher via the Fowler-Noll-Vo hash function.
https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function
string_fnv_hash,
  )
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println(
    "Total compares for \{
Int
n_collision_want} non-colliding keys: \{
Int
n_compares_nc}",
  )
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("")

  //
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("Now, we want all keys to collide into bucket #\{
Int
target_bucket_id}.")
  let 
Array[String]
colliding_keys = 
(bucket_count : Int, target_bucket : Int, n_collision_want : Int, hash_fn : (String) -> UInt) -> Array[String]
find_collision(
    
Int
bucket_count, 
Int
target_bucket_id, 
Int
n_collision_want, 
(s : String) -> UInt
A simple string hasher via the Fowler-Noll-Vo hash function.
https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function
string_fnv_hash,
  )
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("Found \{
Array[String]
colliding_keys.
(self : Array[String]) -> Int
Returns the number of elements in the array.
Parameters:

array : The array whose length is to be determined.
Returns the number of elements in the array as an integer.
Example:
  let arr = [1, 2, 3]
  inspect(arr.length(), content="3")
  let empty : Array[Int] = []
  inspect(empty.length(), content="0")
length()} colliding keys.")
  let 
Int
n_compares_c = 
(n_buckets : Int, keys : Array[String], hash_fn : (String) -> UInt) -> Int
test_attack(
Int
bucket_count, 
Array[String]
colliding_keys, 
(s : String) -> UInt
A simple string hasher via the Fowler-Noll-Vo hash function.
https://en.wikipedia.org/wiki/Fowler%E2%80%93Noll%E2%80%93Vo_hash_function
string_fnv_hash)
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println(
    "Total compares for \{
Int
n_collision_want} colliding keys: \{
Int
n_compares_c}",
  )

  //
  let 
Double
increase = 
Int
n_compares_c.
(self : Int) -> Double
Converts a 32-bit integer to a double-precision floating-point number. The
conversion preserves the exact value since all integers in the range of Int
can be represented exactly as Double values.
Parameters:

self : The 32-bit integer to be converted.
Returns a double-precision floating-point number that represents the same
numerical value as the input integer.
Example:
  let n = 42
  inspect(n.to_double(), content="42")
  let neg = -42
  inspect(neg.to_double(), content="-42")
to_double() 
(self : Double, other : Double) -> Double
Performs division between two double-precision floating-point numbers.
Follows IEEE 754 standard for floating-point arithmetic, including handling
of special cases like division by zero (returns infinity) and operations
involving NaN.
Parameters:

self : The dividend (numerator) in the division operation.
other : The divisor (denominator) in the division operation.
Returns the result of dividing self by other. Special cases follow IEEE
754:

Division by zero returns positive or negative infinity based on the
dividend's sign
Operations involving NaN return NaN
Division of infinity by infinity returns NaN
Example:
  inspect(6.0 / 2.0, content="3")
  inspect(-6.0 / 2.0, content="-3")
  inspect(1.0 / 0.0, content="Infinity")
/ 
Int
n_compares_nc.
(self : Int) -> Double
Converts a 32-bit integer to a double-precision floating-point number. The
conversion preserves the exact value since all integers in the range of Int
can be represented exactly as Double values.
Parameters:

self : The 32-bit integer to be converted.
Returns a double-precision floating-point number that represents the same
numerical value as the input integer.
Example:
  let n = 42
  inspect(n.to_double(), content="42")
  let neg = -42
  inspect(neg.to_double(), content="-42")
to_double()
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("The number of compares increased by a factor of \{
Double
increase}")
}

The output of the code above is:

Demonstrate hash flooding attack
First, try to insert non-colliding keys.
Total compares for 1000 non-colliding keys: 347

Now, with colliding keys...
Found 1000 colliding keys.
Total compares for 1000 colliding keys: 499500
The number of compares increased by a factor of 1439.4812680115274

... as can be seen directly, now the insertion is some 1000 times slower!

In reality, although the number of buckets in hashmaps is not fixed like our examples, they often follow a certain growing sequence, such as doubling or following a list of predefined prime numbers. This growth pattern makes the bucket count very predictable. Thus, an attacker can initiate a hash flooding attack even if they don't know the exact bucket count.

Mitigating hash flooding attacks​

Hash flooding attack works because the attacker knows exactly how a hash function works, and how it connects to where the key is inserted into the hashmap. If we change either of them, the attack will no longer work.

Seeded hash function​

By far, the easiest way to do this is to prevent the attacker from knowing how the hash algorithm exactly works. This might sound impossible, but the properties of the hash function actually only need to hold within a single hashmap!

When dealing with hashmaps, we don't need a single, global "hash value" that can be used everywhere, because hashmaps don't care about what happens outside them. Simply swapping out the hash function from table to table, and you get something that's unpredictable to the attacker.

But hey, you may say, "we don't have an infinite supply of different hash algorithms!"

Well, you do. Remember that hash functions need to distribute the value across the result space as uniform as possible? That means, for a good hash function, a slight change in the input can cause a large change in the output. So, in order to get a hash function unique to each table, we only need to feed it some data unique to the table before feeding it the data we want to hash. This is called a "seed" to the hash function, and each table can now have a different seed to use.

Let's demonstrate how the seed solves the problem with a seeded hash function and two tables with different seeds:

/// A modified version of the FNV hash before to allow a seed to be used.
fn 
(seed : UInt) -> (String) -> UInt
A modified version of the FNV hash before to allow a seed to be used.
string_fnv_hash_seeded(
UInt
seed : 
UInt
UInt) -> (
String
String) -> 
UInt
UInt {
  let 
Bytes
seed_bytes = 
UInt
seed.
(self : UInt) -> Bytes
Converts the UInt to a Bytes in little-endian byte order.
to_le_bytes()
  fn 
(String) -> UInt
string_fnv_hash(
String
s : 
String
String) -> 
UInt
UInt {
    let 
Bytes
s_bytes = 
(str : StringView, bom? : Bool, endianness? : @encoding/utf16.Endian) -> Bytes
Encodes a string into a UTF-16 byte array.
Assuming the string is valid.
@encoding/utf16.encode(
String
s)
    let mut 
UInt
acc : 
UInt
UInt = 0x811c9dc5
    // Mix in the seed bytes.
    for 
Byte
b in 
Bytes
seed_bytes {
      
UInt
acc = (
UInt
acc 
(self : UInt, other : UInt) -> UInt
Performs a bitwise XOR (exclusive OR) operation between two unsigned 32-bit
integers. Each bit in the result is set to 1 if the corresponding bits in the
operands are different, and 0 if they are the same.
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand.
Returns the result of the bitwise XOR operation.
Example:
  let a = 0xFF00U // Binary: 1111_1111_0000_0000
  let b = 0x0F0FU // Binary: 0000_1111_0000_1111
  inspect(a ^ b, content="61455") // Binary: 1111_0000_0000_1111
^ 
Byte
b.
(self : Byte) -> UInt
Converts a Byte to a UInt.
Parameters:

byte : The Byte value to be converted.
Returns the UInt representation of the Byte.
to_uint()) 
(self : UInt, other : UInt) -> UInt
Performs multiplication between two unsigned 32-bit integers. The result
wraps around if it exceeds the maximum value of UInt.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand.
Returns the product of the two unsigned integers. If the result exceeds the
maximum value of UInt (4294967295), it wraps around to the corresponding
value modulo 2^32.
Example:
  let a = 3U
  let b = 4U
  inspect(a * b, content="12")
  let max = 4294967295U
  inspect(max * 2U, content="4294967294") // Wraps around to max * 2 % 2^32
* 0x01000193
    }
    // Hash the string bytes.
    for 
Byte
b in 
Bytes
s_bytes {
      
UInt
acc = (
UInt
acc 
(self : UInt, other : UInt) -> UInt
Performs a bitwise XOR (exclusive OR) operation between two unsigned 32-bit
integers. Each bit in the result is set to 1 if the corresponding bits in the
operands are different, and 0 if they are the same.
Parameters:

self : The first unsigned 32-bit integer operand.
other : The second unsigned 32-bit integer operand.
Returns the result of the bitwise XOR operation.
Example:
  let a = 0xFF00U // Binary: 1111_1111_0000_0000
  let b = 0x0F0FU // Binary: 0000_1111_0000_1111
  inspect(a ^ b, content="61455") // Binary: 1111_0000_0000_1111
^ 
Byte
b.
(self : Byte) -> UInt
Converts a Byte to a UInt.
Parameters:

byte : The Byte value to be converted.
Returns the UInt representation of the Byte.
to_uint()) 
(self : UInt, other : UInt) -> UInt
Performs multiplication between two unsigned 32-bit integers. The result
wraps around if it exceeds the maximum value of UInt.
Parameters:

self : The first unsigned integer operand.
other : The second unsigned integer operand.
Returns the product of the two unsigned integers. If the result exceeds the
maximum value of UInt (4294967295), it wraps around to the corresponding
value modulo 2^32.
Example:
  let a = 3U
  let b = 4U
  inspect(a * b, content="12")
  let max = 4294967295U
  inspect(max * 2U, content="4294967294") // Wraps around to max * 2 % 2^32
* 0x01000193
    }
    
UInt
acc
  }

  
(String) -> UInt
string_fnv_hash
}

test {
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("Demonstrate flooding attack mitigation")
  let 
Int
bucket_count = 2048
  let 
Int
target_bucket_id = 42
  let 
Int
n_collision_want = 1000

  // The first table has a seed of 42.
  let 
UInt
seed1 : 
UInt
UInt = 42
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("We find collisions using the seed \{
UInt
seed1}")
  let 
(String) -> UInt
hash_fn1 = 
(seed : UInt) -> (String) -> UInt
A modified version of the FNV hash before to allow a seed to be used.
string_fnv_hash_seeded(
UInt
seed1)
  let 
Array[String]
colliding_keys = 
(bucket_count : Int, target_bucket : Int, n_collision_want : Int, hash_fn : (String) -> UInt) -> Array[String]
find_collision(
    
Int
bucket_count, 
Int
target_bucket_id, 
Int
n_collision_want, 
(String) -> UInt
hash_fn1,
  )
  let 
Int
n_compares_c = 
(n_buckets : Int, keys : Array[String], hash_fn : (String) -> UInt) -> Int
test_attack(
Int
bucket_count, 
Array[String]
colliding_keys, 
(String) -> UInt
hash_fn1)
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println(
    "Total compares for \{
Int
n_collision_want} colliding keys with seed \{
UInt
seed1}: \{
Int
n_compares_c}",
  )
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println("")

  // The second table has a different seed
  let 
UInt
seed2 : 
UInt
UInt = 100
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println(
    "We now use a different seed for the second table, this time \{
UInt
seed2}",
  )
  let 
(String) -> UInt
hash_fn2 = 
(seed : UInt) -> (String) -> UInt
A modified version of the FNV hash before to allow a seed to be used.
string_fnv_hash_seeded(
UInt
seed2)
  let 
Int
n_compares_nc = 
(n_buckets : Int, keys : Array[String], hash_fn : (String) -> UInt) -> Int
test_attack(
Int
bucket_count, 
Array[String]
colliding_keys, 
(String) -> UInt
hash_fn2)
  
(input : String) -> Unit
Prints any value that implements the Show trait to the standard output,
followed by a newline.
Parameters:

value : The value to be printed. Must implement the Show trait.
Example:
  println(42)
  println("Hello, World!")
  println([1, 2, 3])
println(
    "Total compares for \{
Int
n_collision_want} keys that were meant to collide with seed \{
UInt
seed1}: \{
Int
n_compares_nc}",
  )
}

The output of the program above was:

Demonstrate flooding attack mitigation
We find collisions using 42
Total compares for 1000 colliding keys with seed 42: 499500

We now use a different seed for the second table, this time 100
Total compares for 1000 keys that were meant to collide with seed 42: 6342

We can see that, the keys that were colliding in the first table are not colliding in the second. ³ Therefore, we have successfully mitigated the hash flooding attack using this simple trick.

As of where the seed that randomizes each hashmap comes from... For programs with access to an external random source (like Linux's /dev/urandom), using that would generally be the best choice. For programs without such access (such as within a WebAssembly sandbox), a per-process random seed is also a preferrable solution (this is what Python does). Even simpler, a simple counter that increments with each seeding attempt could be good enough -- guessing how many hashmaps have been created can still be quite hard for an attacker.

Other choices​

Java uses a different solution, by falling back to a binary search tree (red-black tree) when too many values occupy the same bucket. Yes, this requires the keys to be also comparable in addition to being hashable, but now it guarantees $O(\log n)$ worst-case complexity, which is far better than $O(n)$.

Why does it matter to us?​

Due to the ubiquitous nature of hashmaps, it's extremely easy to find some hashmap in a program where you can control the keys, especially in Web programs. Headers, cookies, query parameters and JSON bodies are all key-value pairs, and often stored in hashmaps, which might be vulnerable to hash flooding attacks.

A malicious attacker with enough knowledge of the program (programming language, frameworks, etc.) can then try to send carefully-crafted request payloads to the Web API endpoints. These requests take a lot longer to handle, so if a regular denial-of-service (DoS) attack takes n requests/s to bring down a server, a hash flooding attack might only a tiny fraction of that number, often a magnitude smaller -- making it far more efficient for the attacker. This turns the DoS attack into a HashDoS attack.

Fortunately, by introducing some even slightly unpredictable patterns (such as a per-process randomness or keyed hashing) into hashmaps, we can make such attack significantly harder, often impractical. Also, as such attack is highly dependent on the language, framework, architecture and implementation of target application, crafting one could be quite hard already, and modern, well-configured systems are even more harder to exploit.

Takeaways​

Hashmaps give us powerful, constant-time average access -- but that "constant" depends on assumptions an attacker can sometimes break. A targeted hash-flooding attack forces many keys into the same bucket and turns O(1) operations into O(n), enabling highly efficient resource exhaustion.

The good news is the mitigations are simple and practical: introduce some unpredictableness to your hashmaps, use side-channel information when hash alone is not enough, or rehash when the behavior doesn't look right. With these, we can keep our hashmaps fast and secure.

Footnotes​

1. Side note, this is also similar to how Bitcoin mining works -- finding a value to add to an existing string, so the hash of the entire thing (with bits reversed), modulo some given value, is zero. ↩

2. There's even a Tumblr blog for unexpected quadratic complexity in programming languages, Accidentally Quadratic. You can even find a hashmap-related one here! -- It's almost a manually-introduced hash flooding attack. ↩

3. You may notice that this number is still slightly higher than that we got with randomly-generated, non-colliding keys. This might be related to that FNV is not designed for the best quality of its output. Since the two seeds are pretty close to each other, the result might still have some similarity. Using a better hash function (or even a cryptographically-secure one like SipHash) would greatly reduce this effect. ↩

In this article, I will introduce MoonBit's async programming support and the moonbitlang/async library by writing a simple HTTP file server. If you have experience with the Python language before, you may know that Python has a very convenient builtin HTTP server module. You can launch a HTTP file server sharing current directory by running python -m http.server from the command line, which is useful for LAN file sharing. In this article, we will write a program with similar functionality in MoonBit, and learn about MoonBit's async programming support. We will implement an extra useful functionality absent in python -m http.server: downloading the whole directory as a .zip file.

A brief history of async programming​

Async programming enables programs to perform multiple tasks at the same time. For example, for a file server, there may be many users accessing the server at the same time. The server needs to serve all users at the same time while making the experience of every user as fluent as possible. In a typical async program, such as a server, most time is spent on waiting for IO operations in a single task, and only a small portion of time is spent on actual computation. So, we don't really need a lot of computation power to handle a lot of tasks. The key here is to switch frequently between tasks: if a task starts waiting for IO, don't process it anymore, switch to a task that is immediately ready instead.

In the past, async programming is usually implemented via multi-threading. Every task in the program corresponds to a operating system thread. However, OS threads are resource heavy, the context switch between OS threads is expensive, too. So, today, async programming is usually implemented via event loops. In an event loop based async program, the whole is structured as a big loop. In every iteration of the loop, the program check for a list of completed IO operations, and resume the tasks blocked on these IO operations, until they issue another IO request and enter waiting state again. In this programming paradigm, the context switch between tasks happens in the user space, on a single OS thread. So the cost of switching between tasks is very cheap.

Although event loop solves the performance problem, it is very painful to code event loop based program manually. The code of a single task need to be splitted into multiple iterations of the event loop, damaging the readability of program logic significantly. Fortunately, like most other modern programming languages, MoonBit provides native async programming support. Users can write async code just like normal, synchronous code. The MoonBit compiler will automatically split async code into multiple parts, while the moonbitlang/async library provides the event loop, various IO primitives, and a scheduler that actually runs the async code.

Async programming in MoonBit​

In MoonBit, you can declare an async function using the async fn syntax. Async functions look exactly the same as normal, synchronous functions, except that thay may be interrupted in the middle at run time, so that the program can switch between multiple tasks.

Unlike most other languages, MoonBit doesn't need special marks such as await when calling async functions. The compiler will automatically infer which function calls are async. However, if you read async MoonBit code in a IDE or text editor that supports MoonBit, you can see async function calls rendered in italic style, and function calls that may raise error rendered with underline. So, you can still easily find out all async function calls when reading code.

For async programming, it is also necessary to have an event loop, a task scheduler and various IO primitives. In MoonBit, these are implemented via the moonbitlang/async library. moonbitlang/async provides support for async primitives such as network IO, file IO and process creation, as well as a lot of useful task management facilities. In the following parts, We will learn about various features of moonbitlang/async while writing the HTTP file server.

The structure of a HTTP server​

The structure of a typical HTTP server is:

• the server listen on a TCP socket, waiting for incoming connections from users
• after accepting a TCP connection from a user, the server read the user's request from the TCP connection, process it, and send the result back to the user.

Every task described above must be performed asynchronously: when performing the request from the first user, the server should still keep waiting for new connections, and react to the connection request of the next user. If many users connect to the server at the same time, the server should handle the requests from all users in parallel. When handling user requests, all time consuming operations, such as network IO and file IO, should be asynchronous: they should not block the program and affect the handling of other tasks.

moonbitlang/async provides a helper function @http.run_server, which automatically setup a HTTP server and run it:

async fn 
async (path~ : String, port~ : Int) -> Unit
server_main(
String
path~ : 
String
String, 
Int
port~ : 
Int
Int) -> 
Unit
Unit {
  
(Unit, (?, Unit) -> Unit) -> Unit
@http.run_server(
(String) -> Unit
@socket.Addr::parse("[::]:\{
Int
port}"), fn (
?
conn, 
Unit
addr) {
    
Unit
@pipe.stderr.
(String) -> Unit
write("received new connection from \{
Unit
addr}\n")
    
async (base_path : String, conn : ?) -> Unit
handle_connection(
String
path, 
?
conn)
  })
}

server_main accepts two parameters. path is the directory to serve, and port is the port to listen on. In moonbitlang/async, all async code are cancellable, and cancellation is performed by raising an error in cancelled code. So, MoonBit assumes all async fn may raise error by default, eliminating the need for explicitly marking async fn with raise.

In server_main, we use @http.run_server to create a HTTP server and run it. @http is the default alias for moonbitlang/async/http, which provides HTTP support for moonbitlang/async. The first parameter of @http.run_server is the address to listen, here we ask the server to listen on [::]:port, which means listening on port on any network interface. moonbitlang/async provides native IPv4/IPv6 dual stack support, so the server here can accept both IPv4 connections and IPv6 connections. The second parameter of @http.run_server is a callback function used for handling client request. The callback function receives two parameters, the first one is the connection from the user, represented using the type @http.ServerConnection. The connection is created automatically by @http.run_server. The second parameter of the callback function is the network address of the user. Here, we use a function handle_connection to handle the request, the implementation of handle_connection will be given later. @http.run_server will automatically create a new task, and run handle_connection in the new task. So, the server may run multiple instances handle_connection in parallel, handling multiple user connections at the same time.

Handle user request​

Now, let's implement the handle_connection function. handle_connection accepts two parameters: base_path is the directory being served, and conn is the connection from the user. The implementation of handle_connection is as follows:

async fn 
async (base_path : String, conn : ?) -> Unit
handle_connection(
  
String
base_path : 
String
String,
  
?
conn : @http.ServerConnection,
) -> 
Unit
Unit {
  for {
    let 
Unit
request = 
?
conn.
() -> Unit
read_request()
    
?
conn.
() -> Unit
skip_request_body()
    guard 
Unit
request.
Unit
meth is 
Unit
Get else {
      
?
conn
      ..
(Int, String) -> Unit
send_response(501, "Not Implemented")
      ..
(String) -> Unit
write("This request is not implemented")
      ..
() -> Unit
end_response()
    }
    let (
String
path, 
Bool
download_zip) = match 
Unit
request.
String
path {
      
String
[ ..path, .."?download_zip" ] => (
StringView
path.
(self : StringView) -> String
Returns a new String containing a copy of the characters in this view.
Examples
  let str = "Hello World"
  let view = str.view(start_offset = str.offset_of_nth_char(0).unwrap(),end_offset = str.offset_of_nth_char(5).unwrap()) // "Hello"
  inspect(view.to_string(), content="Hello")
to_string(), true)
      
String
path => (
String
path, false)
    }
    if 
Bool
download_zip {
      
async (conn : ?, path : String) -> Unit
serve_zip(
?
conn, 
String
base_path 
(self : String, other : String) -> String
Concatenates two strings, creating a new string that contains all characters
from the first string followed by all characters from the second string.
Parameters:

self : The first string to concatenate.
other : The second string to concatenate.
Returns a new string containing the concatenation of both input strings.
Example:
  let hello = "Hello"
  let world = " World!"
  inspect(hello + world, content="Hello World!")
  inspect("" + "abc", content="abc") // concatenating with empty string
+ 
String
path)
    } else {
      let 
?
file = 
(String, Unit) -> ?
@fs.open(
String
base_path 
(self : String, other : String) -> String
Concatenates two strings, creating a new string that contains all characters
from the first string followed by all characters from the second string.
Parameters:

self : The first string to concatenate.
other : The second string to concatenate.
Returns a new string containing the concatenation of both input strings.
Example:
  let hello = "Hello"
  let world = " World!"
  inspect(hello + world, content="Hello World!")
  inspect("" + "abc", content="abc") // concatenating with empty string
+ 
String
path, 
Unit
mode=
Unit
ReadOnly) catch {
        _ => {
          
?
conn
          ..
(Int, String) -> Unit
send_response(404, "NotFound")
          ..
(String) -> Unit
write("File not found")
          ..
() -> Unit
end_response()
          continue
        }
      }
      defer 
?
file.
() -> Unit
close()
      if 
?
file.
() -> Unit
kind() is 
Unit
Directory {
        if 
Bool
download_zip {
        } else {
          
async (conn : ?, dir : ?, path~ : String) -> Unit
serve_directory(
?
conn, 
?
file.
() -> ?
as_dir(), 
String
path~)
        }
      } else {
        
async (conn : ?, file : ?, path~ : String) -> Unit
server_file(
?
conn, 
?
file, 
String
path~)
      }
    }
  }
}

In handle_connection, the program read requests from the user connection and handle them in a big loop. In every iteration, we first read the next request from the user via conn.read_request(). conn.read_request() will only read the header part of a HTTP request, in order to allow streaming read for large body in user request. Since our file server only handles GET request, the body of requests is irrelevant. So, we use conn.skip_body() to skip the body of user request, so that the content of the next request can be processed normally.

If we meet a request that is not GET, the else block of guard statement will be executed. Code after the guard statement will be skipped, and the program will enter the next iteration directly and handle the next request. In the else block, we use conn.send_response(..) to send a "NotImplemented" response back to the user. conn.send_response(..) will only send the header part of the response. After send_response, we use conn.write(..) to write the body of the response to the connection. After writing all desired contents, we use conn.end_response() to tell the library that the response body has completed.

Here, we want to implement a useful feature absent in python -m http.server: download the whole directory as a zip file. If the requested URL has the shape /path/to/directory?download_zip, we package /path/to/directory into a .zip file and send it to the user. This feature is implemented using the serve_zip function to be given later.

Since we are implementing a file server, the requested path in users' GET request will map to file system path under base_path directly. @fs is the default alias of moonbitlang/async/fs, the package for file system IO support in moonbitlang/async. Here, we use @fs.open to open the requested file. In the @fs.open operation fails, we send the user a 404 response, notifying the user that the requested file does not exist.

If the requested file is successfully opened, we need to send its content to the user. Before that, we use defer file.close() to ensure that the opened file will be closed correctly. We can obtain the kind of the file via file.kind(). In a file server, directories need some special handling. Since we cannot send a directory over network, we need to serve a HTML page for the user, which contains the contents of the directory, and links that jump to the corresponding page of each file in the directory. This part of the server is implemented in the serve_directory function, whose definition will be provided later.

If the requested file is a regular file, we simply send the content of the file to the user. This is implemented via the serve_file function:

async fn 
async (conn : ?, file : ?, path~ : String) -> Unit
server_file(
  
?
conn : @http.ServerConnection,
  
?
file : @fs.File,
  
String
path~ : 
String
String,
) -> 
Unit
Unit {
  let 
String
content_type = match 
String
path {
    [.., .. ".png"] => "image/png"
    [.., .. ".jpg"] | "jpeg" => "image/jpeg"
    [.., .. ".html"] => "text/html"
    [.., .. ".css"] => "text/css"
    [.., .. ".js"] => "text/javascript"
    [.., .. ".mp4"] => "video/mp4"
    [.., .. ".mpv"] => "video/mpv"
    [.., .. ".mpeg"] => "video/mpeg"
    [.., .. ".mkv"] => "video/x-matroska"
    _ => "appliaction/octet-stream"
  }
  
?
conn
  ..
(Int, String, Map[String, String]) -> Unit
send_response(200, "OK", 
Map[String, String]
extra_headers={ "Content-Type": 
String
content_type })
  ..
(?) -> Unit
write_reader(
?
file)
  ..
() -> Unit
end_response()
}

In the HTTP response header, we fill in different values for the Content-Type field based on the suffix of the requested file. With correct Content-Type, the users can view the content of image/video/HTML file in the browser directly. For other files, the value of Content-Type is set to application/octet-stream, which tells the browser to download the file automatically.

As before, we use conn.send_response to send the response header. The extra_headers field allows us to set extra header fields for the response. The body of the response is the content of the file. Here, conn.write_reader(..) will send the content of file to the user streamingly. Assume the user requests for a video file and plays it in the browser, if we read the whole video file in memory first before sending it to the user, the user can only see response from the server after the whole video file has been loaded, resulting in poor latency. It is also a huge waste of memory to load the whole video file. write_reader, on the other hand, automatically split the file into small chunks, and send the content of the file chunk-by-chunk. This way, users can start playing the video immediately, and the server can save up a lot of memory.

Next, let's implement the serve_directory function:

async fn 
async (conn : ?, dir : ?, path~ : String) -> Unit
serve_directory(
  
?
conn : @http.ServerConnection,
  
?
dir : @fs.Directory,
  
String
path~ : 
String
String,
) -> 
Unit
Unit {
  let 
Unit
files = 
?
dir.
() -> Unit
read_all()
  
Unit
files.
() -> Unit
sort()
  
?
conn
  ..
(Int, String, Map[String, String]) -> Unit
send_response(200, "OK", 
Map[String, String]
extra_headers={ "Content-Type": "text/html" })
  ..
(String) -> Unit
write("<!DOCTYPE html><html><head></head><body>")
  ..
(String) -> Unit
write("<h1>\{
String
path}</h1>\n")
  ..
(String) -> Unit
write("<div style=\"margin: 1em; font-size: 15pt\">\n")
  ..
(String) -> Unit
write("<a href=\"\{
String
path}?download_zip\">download as zip</a><br/><br/>\n")
  if 
String
path[:-1].
(self : StringView, str : StringView) -> Int?
Returns the offset of the last occurrence of the given substring. If the
substring is not found, it returns None.
rev_find("/") is 
(Int) -> Int?
Some(
Int
index) {
    let 
String
parent = if 
Int
index 
(self : Int, other : Int) -> Bool
Compares two integers for equality.
Parameters:

self : The first integer to compare.
other : The second integer to compare.
Returns true if both integers have the same value, false otherwise.
Example:
  inspect(42 == 42, content="true")
  inspect(42 == -42, content="false")
== 0 { "/" } else { 
String
path[:
Int
index].
(self : StringView) -> String
Returns a new String containing a copy of the characters in this view.
Examples
  let str = "Hello World"
  let view = str.view(start_offset = str.offset_of_nth_char(0).unwrap(),end_offset = str.offset_of_nth_char(5).unwrap()) // "Hello"
  inspect(view.to_string(), content="Hello")
to_string() }
    
?
conn.
(String) -> Unit
write("<a href=\"\{
String
parent}\">..</a><br/><br/>\n")
  }
  for 
Unit
file in 
Unit
files {
    let 
String
file_url = if 
String
path
(String, Int) -> Int
Returns the UTF-16 code unit at the given index.
Parameters:

string : The string to access.
index : The position in the string from which to retrieve the code unit.
This method has O(1) complexity.
[path.
(self : String) -> Int
Returns the number of UTF-16 code units in the string. Note that this is not
necessarily equal to the number of Unicode characters (code points) in the
string, as some characters may be represented by multiple UTF-16 code units.
Parameters:

string : The string whose length is to be determined.
Returns the number of UTF-16 code units in the string.
Example:
  inspect("hello".length(), content="5")
  inspect("🤣".length(), content="2") // Emoji uses two UTF-16 code units
  inspect("".length(), content="0") // Empty string
length() 
(self : Int, other : Int) -> Int
Performs subtraction between two 32-bit integers, following standard two's
complement arithmetic rules. When the result overflows or underflows, it
wraps around within the 32-bit integer range.
Parameters:

self : The minuend (the number being subtracted from).
other : The subtrahend (the number to subtract).
Returns the difference between self and other.
Example:
  let a = 42
  let b = 10
  inspect(a - b, content="32")
  let max = 2147483647 // Int maximum value
  inspect(max - -1, content="-2147483648") // Overflow case
- 1] 
(x : Int, y : Int) -> Bool
!= '/' {
      "\{
String
path}/\{
Unit
file}"
    } else {
      "\{
String
path}\{
Unit
file}"
    }
    
?
conn.
(String) -> Unit
write("<a href=\"\{
String
file_url}\">\{
Unit
file}</a><br/>\n")
  }
  
?
conn
  ..
(String) -> Unit
write("</div></body></html>")
  ..
() -> Unit
end_response()
}

Here, we first read the list of files in the directory and sort them. Next, we build a HTML page based on the content of the directory. The body of the HTML page is the list of files in the directory, each file corresponds to a <a> HTML link showing the name of the file. Users can jump to the page of the file by clicking the link. If the requested directory is not the root directory, we add a special link .. at the beginning of the page, which jumps to the parent directory of current directory. Finally, the page also contains a download as zip link, which jumps to the zip download URL for current directory.

Implement the download as zip feature​

Finally, let's implement the "download as zip" feature. Here, for simplicity, we use the zip command for compression. The implementation of serve_zip is as follows:

async fn 
async (conn : ?, path : String) -> Unit
serve_zip(
  
?
conn : @http.ServerConnection,
  
String
path : 
String
String,
) -> 
Unit
Unit {
  let 
Unit
full_path = 
(String) -> Unit
@fs.realpath(
String
path)
  let 
String
zip_name = if 
Unit
full_path[:].
(String) -> Unit
rev_find("/") is 
(Int) -> Unit
Some(
Int
i) {
    
Unit
full_path[
Int
i+1:].
() -> String
to_string()
  } else {
    
String
path
  }
  
((Unit) -> Unit) -> Unit
@async.with_task_group(fn(
Unit
group) {
    let (
Unit
we_read_from_zip, 
Unit
zip_write_to_us) = 
() -> (Unit, Unit)
@process.read_from_process()
    defer 
Unit
we_read_from_zip.
() -> Unit
close()
    
Unit
group.
(() -> Unit) -> Unit
spawn_bg(fn() {
      let 
Int
exit_code = 
(String, Array[String], Unit) -> Int
@process.run(
        "zip",
        [ "-q", "-r", "-", 
String
path ],
        
Unit
stdout=
Unit
zip_write_to_us,
      )
      if 
Int
exit_code 
(x : Int, y : Int) -> Bool
!= 0 {
        
(msg : String, loc~ : SourceLoc = _) -> Unit raise Failure
Raises a Failure error with a given message and source location.
Parameters:

message : A string containing the error message to be included in the
failure.
location : The source code location where the failure occurred.
Automatically provided by the compiler when not specified.
Returns a value of type T wrapped in a Failure error type.
Throws an error of type Failure with a message that includes both the
source location and the provided error message.
fail("zip failed with exit code \{
Int
exit_code}")
      }
    })
    
?
conn
    ..
(Int, String, Map[String, String]) -> Unit
send_response(200, "OK", 
Map[String, String]
extra_headers={
      "Content-Type": "application/octet-stream",
      "Content-Disposition": "filename=\{
String
zip_name}.zip",
    })
    ..
(Unit) -> Unit
write_reader(
Unit
we_read_from_zip)
    ..
() -> Unit
end_response()
  })
}

At the beginning of serve_zip, we first compute the file name for the .zip file. Next, we create a new task group using @async.with_task_group. Task group is the core construct for task management in moonbitlang/async, all tasks must be spawned in a task group. But before we get into the details of with_task_group, let's first check out the remaining content of serve_zip. First, we use @process.read_from_process to create a temporary pipe. Data written to one end of the pipe can be read from the other end, so the pipe can be used to obtain the output of a system command. We will pass the write end of the pipe, zip_write_to_us to the zip command, and let zip write the result of compression to zip_write_to_us. Meanwhile, we will read the output of the zip command from the read end of the pipe, we_read_from_zip, and send the result to the user.

To accomplish the above job, we first spawn a new task in the task group using growp.spawn_bg(..). group.spawn_bg(..) accepts a function as argument, and run the function in a new background task, in parallel with other code in the program. Within the new task, we wse @process.run to launch the zip command. @process is the default alias of moonbitlang/async/process, which provides process spawning and manipulation support for moonbitlang/async. The meaning of the arguments of zip is:

• -q: do not output log
• -r: recursively compress the whole directory
• -: write the result of compression to stdout
• path: the directory to compress

When launching zip with @process.run, the stdout=zip_write_to_us part redirects the stdout of zip to zip_write_to_us, so that we can obtain the output of zip. Compared to creating a temporary .zip file to store the result, using a pipe is more efficient because:

• the data exchange with zip is completely in-memory, which is more efficient than disk IO
• we can send partial compression result on-the-fly while zip is still working, reducing latency

@process.run will wait until zip finishes and return the exit code of zip. If the zip command fail with a non-zero exit code, we raise an error.

Outside the new task in spawn_bg, we use conn.send_response(..) to initiate a response to the user, and send the output of zip to the user via conn.write_reader(we_read_from_zip). The Content-Disposition HTTP header allows us to specify the file name for the .zip file. This part of code will be run in parallel with the @process.run task.

So far everything looks reasonable. But why do we need to create a new task group here? Why doesn't moonbitlang/async just provide a global task-spawning API, like many other languages do? There is a phenomenon in async programming: it is relatively easy to write an async program that works correctly when everything goes well, but much harder to write an async program that behaves correctly when things go wrong. For the serve_zip example:

• what should we do if the zip command fails?
• what should we do if some network error occurs, or the user closes the connection?

If the zip command fails, the whole serve_zip function should fail too. Since the user already received some incomplete data, it is hard to recover the connection back to normal state, so we have to close the whole connection. If network error occurs when sending data, we should stop the zip command immediately, because its result is no longer useful. Keep the zip command running is just a waste of resource. In the worst case, the pipe for communication with zip may get filled up since we are no longer reading from it, and zip may get blocked forever on writing to the pipe and become a zombie process.

In the code above, we did not perform any explicit error handling. However, when the aforementioned error cases occur, our program can behave correctly and handle all edge cases. The magic lies in the @async.with_task_group function, and the structured concurrency paradigm behind it. The semantic of @async.with_task_group(f) is as follows:

• it will create a new task group group, and run f(group) inside the new group
• f can spawn new tasks in the group via group.spawn_bg(..)
• with_task_group will only return after all tasks inside the group terminates
• if any task inside the group fails, with_task_group will fail as well, and all other remaining tasks in the group is automatically cancelled

The last point here is the key to ensure correct error handling behavior:

• if the zip command fails, the task that calls @process.run will raise an error, failing the whole task. The error will be propagated to the whole task group since no one is catching it. with_task_group will automatically cancel the response-sending task, propagate the error upwards and close the connection.
• if network error occurs, the main response-sending task will fail. The error will also get propagated to the whole task group, and the zip task will be cancelled. When @process.run is cancelled, it automatically terminates the zip command by sending a SIGTERM signal

So, when writing async program using moonbitlang/async, users only need to insert task groups at appropriate places based on the structure of the program, all the remaining error handling details are automatically handled by with_task_group. This is the power of the structured concurrency paradigm of moonbitlang/async: it guides users to write async programs with clearer structure, and makes program behave correctly even when things go wrong.

Run the server​

We have implemented all features of the HTTP file server, now we can actually run the server. MoonBit provides native support for async code, users can use async fn main to define entry point to async program, or use async test to test async code directly. Here, we let the HTTP server serve the content of current working directory, and let it listen on port 8000:

async test {
  
async (path~ : String, port~ : Int) -> Unit
server_main(
String
path=".", 
Int
port=8000)
}

To use the file server, just run the source code of this document via moon test /path/to/this/document.mbt.md, and open the address http://127.0.0.1:8000 in your browser.

Other features of moonbitlang/async can be found in its API document and GitHub repo.